A year ago, I switched to the English Colemak layout. I had developed some bad habits with QWERTY, and I found it easier to learn touch typing on a completely new layout than to correct my old muscle memory. While my English typing improved, the switch unfortunately degraded my Arabic typing experience.
This led me to a question: why not design a new, optimal Arabic keyboard layout from the ground up?
This post is a methodological attempt to build one. The final layout depends on the text corpus used for training and the defined costs for finger and hand movements.
Criteria¶
The design of this keyboard layout is guided by the following principles:
Hand Alternation: Alternate between hands as much as possible to increase typing speed and reduce fatigue.
Home Row Priority: Place the most common letter combinations on the home row for easy access.
Bottom Row Deprioritization: Relegate the least common letters to the less accessible bottom row.
Handedness: Favor one hand over the other (in my case, the right hand).
Adjacent Finger Avoidance: Avoid using adjacent fingers for frequent bigrams (two-letter sequences).
Inward-to-Outward Flow: Prefer typing motions that flow from the outer fingers (pinkie) toward the inner fingers (index and middle).
Finger Strength: Assign more frequent letters to stronger fingers.
To model this problem, we need to define four key components:
Keyboard Representation: A digital model of the physical keyboard.
Layout Representation: A way to represent the assignment of letters to keys.
Evaluation Metric: A function to score the “effort” of a given layout.
Optimization Algorithm: A method to find the layout with the lowest effort.
Keyboard Representation¶
We’ll use Keyboard Layout Editor to visualize and define the keyboard.
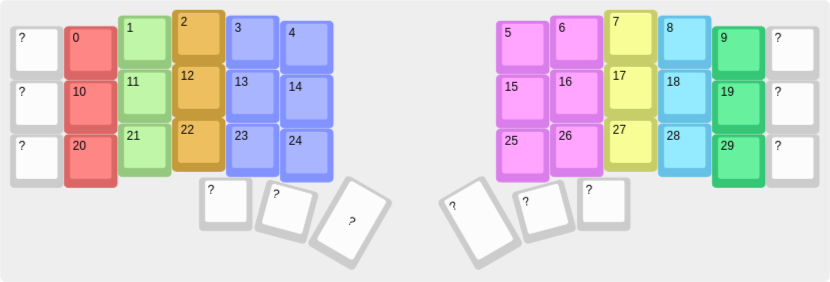
Each key is assigned to a finger, represented by a unique color.
fin2idx = {
"#da6666": 0, "#95c97e": 1, "#c49a3a": 2, "#8292ff": 3,
"#d97eea": 4, "#c7ce69": 5, "#67c0e5": 6, "#35c676": 7,
}
class Finger:
def __init__(self, index):
self.index = index
# start from the home key
self.current_key = index + 10 + (index >= 4)
self.hand = index // 4
self.keys = []
self.costs = {}
def register_key(self, key):
self.keys.append(key)
def precompute_costs(self, theta, phi):
for key1 in self.keys:
for key2 in self.keys:
cost = (
theta * (key1.x - key2.x) ** 2
+ phi[key2.row] * (key1.y - key2.y) ** 2
)
self.costs[(key1.index, key2.index)] = cost**0.5
def __repr__(self):
return str(self.__dict__)The finger starts at its home row key, and every movement to another key has an associated cost. These costs are subjective. For example, moving the pinkie from key 10 to 0 would cost more than moving the index finger from 13 to 3.
Next, we define the Key representation:
class Key:
def __init__(self, index, x, y, finger):
self.index = index
self.x = x
self.y = y
self.finger = finger
self.row = index // 10
finger.register_key(self)
def __repr__(self):
return str(self.__dict__)First, let’s parse the keyboard layout into our Python script. We’ll use pykle_serial to deserialize the JSON data from the Keyboard Layout Editor and instantiate our Key objects:
# download the json from KLE website above
kbd_data = json.load(open("./keyboard.json", "r"))
kbd = kle.serial.deserialize(kbd_data)
keys = []
for key in kbd.keys:
# ignore keys without a color
if key.color in fin2idx:
keys.append(
Key(int(key.labels[0]), x=key.x, y=key.y, finger=fin2idx[key.color])
)Layout Representation¶
The layout is an assignment of each character to a group of letters. Here are our initial groups:
| Group | L1 | L2 | Group | L1 | L2 | Group | L1 | L2 |
|---|---|---|---|---|---|---|---|---|
| 0 | ا | أ | 10 | ز | 20 | ق | ||
| 1 | ب | 11 | س | 21 | ك | |||
| 2 | ت | 12 | ش | 22 | ل | |||
| 3 | ث | 13 | ص | 23 | م | |||
| 4 | ج | 14 | ض | 24 | ن | |||
| 5 | ح | 15 | ط | 25 | ه | |||
| 6 | خ | 16 | ظ | 26 | و | ؤ | ||
| 7 | د | 17 | ع | 27 | ي | ى | ||
| 8 | ذ | 18 | غ | 28 | ء | إ | ||
| 9 | ر | 19 | ف | 29 | ة |
Let’s see if we can improve these assignments.
Corpus¶
I’m going to use a Harakat-free Quran corpus. Let’s look at the letter frequencies.
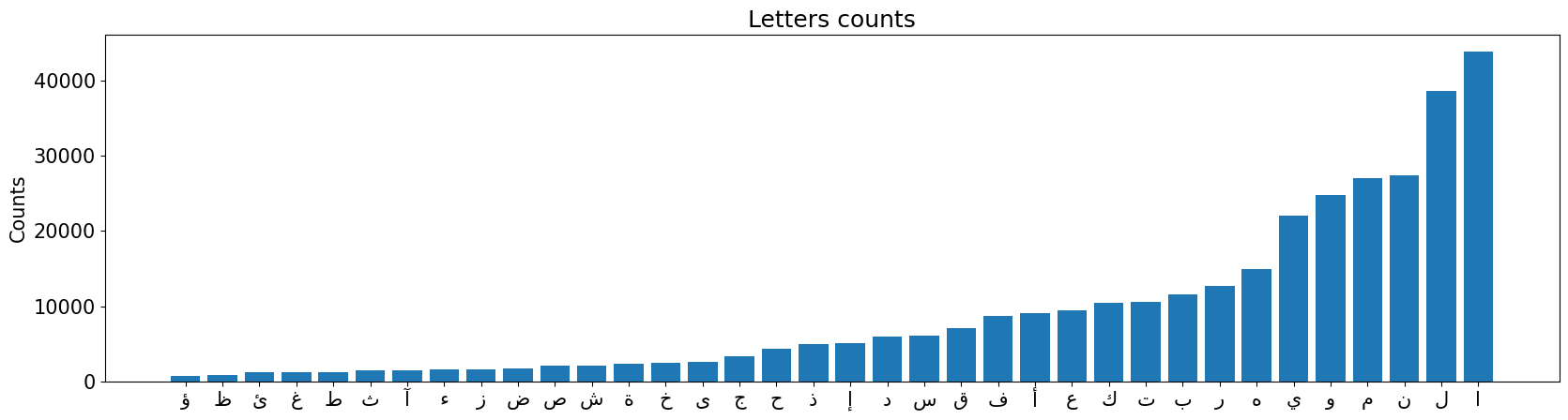
Now, let’s update our groups to move the less frequent letters to Layer 2 (the shifted layer):
Group 26 (و/ؤ) was a good initial guess.
Combine Group 15 (ط) and 16 (ظ).
Combine 18 (غ) and 17 (ع). Since غ is very rare, move it to the second layer of ط/ظ’s group.
Create a new group for ئ and ى (Group 28) and offset the others.
أ is also frequent, so move it to its own group (29) and add آ.
Here is the revised grouping:
| Group | L1 | L2 | Group | L1 | L2 | Group | L1 | L2 |
|---|---|---|---|---|---|---|---|---|
| 0 | ا | 9 | س | 18 | م | |||
| 1 | ب | 10 | ش | 19 | ن | |||
| 2 | ت | ث | 11 | ص | ض | 20 | ه | |
| 3 | ج | 12 | ط | ظ | 21 | و | ؤ | |
| 4 | ح | 13 | ع | غ | 22 | ي | ||
| 5 | خ | 14 | ف | 23 | إ | ء | ||
| 6 | د | 15 | ق | 24 | ة | |||
| 7 | ذ | 16 | ك | 25 | ى | ئ | ||
| 8 | ر | ز | 17 | ل | 26 | أ | آ |
Now we will encode the text using these groups:
corpus = "".join(open("quran.txt", "r").readlines()).replace(" ", "").replace("\n", "")
counts_dict = dict(sorted(collections.Counter(corpus).items(), key=lambda x: x[1]))
groups = {
"ا": 0, "ب": 1, "ت": 2, "ث": 3, "ج": 4, "ح": 5, "خ": 6, "د": 7, "ذ": 8, "ر": 9,
"ز": 10, "س": 11, "ش": 12, "ص": 13, "ض": 14, "ط": 15, "ظ": 15, "ع": 16, "غ": 16,
"ف": 17, "ق": 18, "ك": 19, "ل": 20, "م": 21, "ن": 22, "ه": 23, "و": 24, "ؤ": 24,
"ي": 25, "إ": 26, "ء": 26, "ة": 27, "ى": 28, "ئ": 28, "أ": 29, "آ": 29,
}
codified = []
for c in corpus:
codified.append(groups[c])Layout Evaluation¶
Each layout is a permutation of 30 keys and 30 character groups, assigning each group to a key. Each group inherits the attributes of its assigned key (finger, row, coordinates, hand).
A key detail is that a finger’s position is reset to its home key if it hasn’t been used in the last three keystrokes.
We evaluate each permutation based on an “effort measure,” which we define as follows:
I start from finger .
Now, I need to press the key , which is assigned to finger .
has to move to the position of key , denoted as .
The cost of this movement is:
Cost breakdown¶
is the multiplier for switching from finger to . If the fingers are on different hands, the multiplier is 1, encouraging hand alternation (Criterion 1). If they are on the same hand, the cost increases with the distance between them (Criterion 5). We also prefer movements toward the middle finger (Criterion 6).
# gamma * np.abs(np.arange(4)[:, None] - np.arange(4)[None, :])
alpha_left = gamma * np.array([
[1.5, 1, 0.8, 0.6],
[1, 1.2, 1, 0.8],
[0.8, 1, 1.5, 1.2],
[0.8, 0.6, 1, 1.5]
])
# define the larger alpha
alpha = np.block([[alpha_left, np.zeros((4, 4))], [np.zeros((4, 4)), alpha_left]])is a multiplier for moving finger F. Pinkie movement is less desirable, so it has a higher than other fingers (Criteria 7 & 4).
is the distance of the movement. We can use a modified Euclidean distance that penalizes lateral movements more than vertical ones () and also penalizes moving to the lower row (Criteria 2 & 3).
We have 9 symmetric (or 13 total) hyperparameters to tune:
: finger switching scale
: lateral movement scale
: finger use cost (4 if symmetric, 8 otherwise)
: row cost (3)
To avoid redundant computations, we pre-compute the term for all finger-key pairs after selecting the hyperparameters.
Optimization: Simulated Annealing¶
We use simulated annealing to find the optimal layout:
Start with a random permutation
pand an initial temperature .Evaluate
pto get its costc.For each iteration :
a. Pick a random integer ( is search depth)
b. For
ntimes, make a random modification top(e.g., swap two items or two columns).c. Evaluate the modified permutation to get its cost .
d. Sample a random number .
e. If , accept the new permutation.
f. Decrease the temperature: .
Layout Optimization¶
Hyperparameters¶
: 0.7
: 1.7
: [2, 1.5, 1.2, 1.0, 0.9, ..., 1.8]
: 0.7
Standard Arabic Layout: Cost 866,184¶
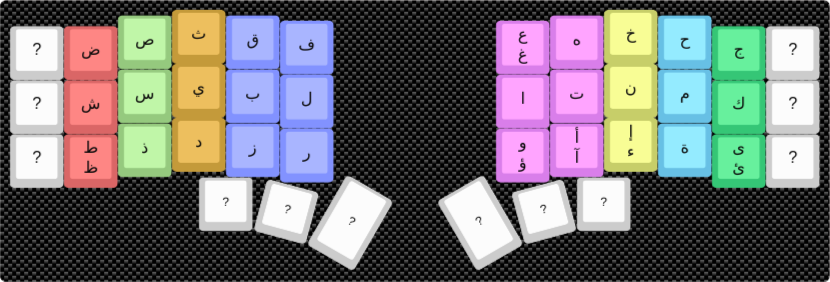
Optimized Layout: Cost 481,506¶
This layout achieves a 45.6% reduction in effort compared to the standard layout.
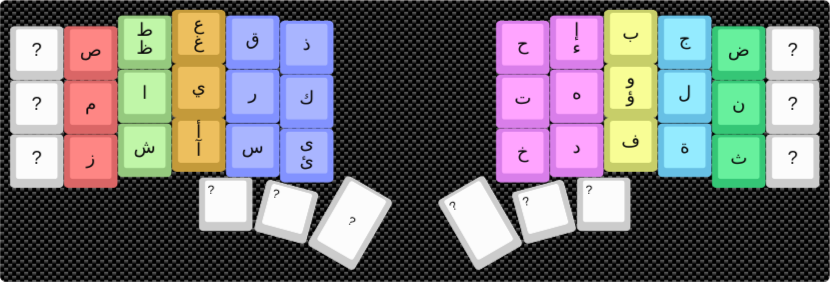
Modified Optimal Layout (with Key Symmetry)¶
This version has a cost of 501,631, a 43% improvement over the standard layout. It’s a cleaner design that places similar-sounding or related letters on symmetric keys (e.g., ق/ف, س/ش).
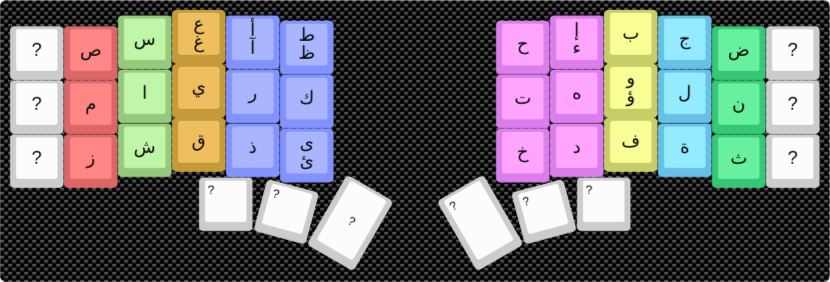
You can try it out here: Link to layout
Future Work¶
This analysis doesn’t yet account for keyboard layers. Moving from one layer to another (e.g., by pressing Shift) incurs a “layer switch” cost that should be incorporated into the model for a more complete optimization.